Enzyme Kinetics: Kinetic Study of Enzymatic Reactions

Enzyme kinetics is a fascinating and crucial area of study in the life sciences, providing insights into how enzymes catalyze biochemical reactions with remarkable specificity and efficiency. Understanding enzyme kinetics is essential for fields ranging from biochemistry and molecular biology to pharmacology and biotechnology.

Kinetic studies on enzymes that only bind one substrate, such as triosephosphate isomerase, aim to measure the affinity with which the enzyme binds this substrate and the turnover rate.

Some other examples of enzymes are phosphofructokinase and hexokinase, both of which are important for cellular respiration (glycolysis).

This article delves into the fundamentals of enzyme kinetics, exploring key concepts, mathematical models, and practical applications. By the end, you’ll have a comprehensive understanding of this vital topic, optimized for SEO to ensure it reaches a broad audience.

• Glycolysis: Glucose Catabolic Pathway
• Chemical Mechanisms of Enzyme Catalysis

What is Enzyme Kinetics?

Enzyme kinetics is the study of the rates at which enzymatic reactions occur. Enzymes are biological catalysts that accelerate chemical reactions by lowering the activation energy required for the reaction to proceed. They do this without being consumed in the process, making them highly efficient and reusable.

The Importance of Enzyme Kinetics

Understanding enzyme kinetics is crucial for several reasons:

1. Drug Development: Many drugs function by inhibiting specific enzymes. Knowledge of enzyme kinetics helps in designing effective inhibitors.
2. Metabolic Engineering: By manipulating enzyme kinetics, scientists can optimize metabolic pathways for industrial applications, such as biofuel production.
3. Diagnostic Tools: Enzyme activity assays are used in clinical diagnostics to detect diseases and monitor treatment efficacy.
4. Basic Research: Enzyme kinetics provides insights into the mechanisms of biochemical reactions, contributing to our understanding of cellular processes.

Enzymes with single-substrate mechanisms include isomerases such as triosephosphate isomerase or bisphosphoglycerate mutase, intramolecular lyases such as adenylate cyclase and the hammerhead ribozyme, an RNA lyase.

However, some enzymes that only have a single substrate do not fall into this category of mechanisms. Catalase is an example of this, as the enzyme reacts with the first molecule of hydrogen peroxide substrate, becomes oxidized and is then reduced by a second molecule of substrate.

• Enzyme Regulation and its Types
• Isoenzymes are Special Proteins with Catalytic activity. Why? (MCQ)

Although a single substrate is involved, the existence of a modified enzyme intermediate means that the mechanism of catalase is actually a ping–pong mechanism, a type of mechanism that is discussed in the Multi-substrate reactions section below.

Enzyme kinetics studies the speed of the reactions catalyzed by enzymes. These studies provide direct information about the mechanism of the catalytic reaction and the specificity of the enzyme. 

The rate of a reaction catalyzed by an enzyme can be measured relatively easily since in many cases it is not necessary to purify or isolate the enzyme. 

The measurement is always made in the optimum conditions of pH, temperature, the presence of co-factors, etc., and saturating concentrations of the substrate are used. 

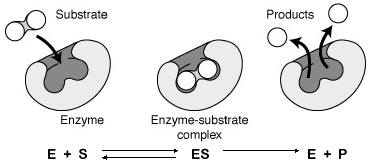
Under these conditions, the observed rate of reaction is the maximum velocity (V _max). The speed can be determined by measuring the appearance of the products or the disappearance of the reactants.

To study enzyme kinetics were measured the effect of the initial concentration of substrate on the initial rate of reaction while maintaining constant the amount of enzyme. 

Denoting v ₀ versus [S] ₀ obtain a graph like that of Figure on the right. When [S] ₀ is small, the initial velocity is directly proportional to the substrate concentration, and therefore, the reaction is first order.

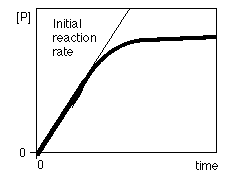
At high [S] ₀, the enzyme is saturated with substrate, and the speed does not depend on [S] 0. At this point, the reaction is zero-order and the maximum speed (V _max ).

Key Concepts in Enzyme Kinetics

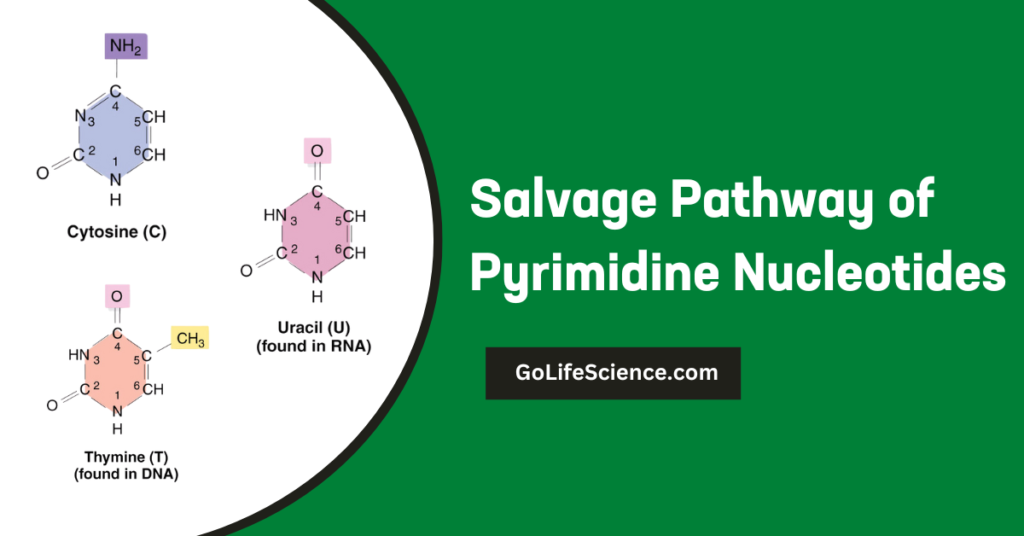
1. Enzyme-Substrate Complex

The interaction between an enzyme (E) and its substrate (S) forms an enzyme-substrate complex (ES). This complex is transient and leads to the formation of the product (P) and the regeneration of the enzyme.

E + S ⇌ ES → E + P

2. Active Site

The active site is the region of the enzyme where the substrate binds and the catalytic reaction occurs. It is highly specific, often described by the “lock and key” or “induced fit” models.

3. Catalytic Efficiency

Catalytic efficiency is a measure of how effectively an enzyme converts substrate into product. It is often expressed as the ratio of the turnover number (kcatkcat​) to the Michaelis constant (KMKM​).

4. Turnover Number (kcatkcat​)

The turnover number represents the maximum number of substrate molecules converted to product per enzyme molecule per unit time. It is a direct measure of the enzyme’s catalytic activity.

5. Michaelis Constant (KM​)

The Michaelis constant is the substrate concentration at which the reaction rate is half of its maximum value (VmaxVmax​). It provides insight into the enzyme’s affinity for the substrate.

6. Initial Rate (V0​)

The initial rate of the reaction is the rate at which product is formed at the beginning of the reaction when the substrate concentration is highest, and the product concentration is negligible.

Mathematical Models in Enzyme Kinetics

1. Michaelis–Menten kinetics

In 1913, Linor Michaelis  (1875-1949) and Maud Menten (1879-1960) put forward the enzyme-substrate complex theory. According, the enzyme (E) combines with the substrate (S), to form an enzyme-substrate (ES) complex, which immediately breaks down to the Enzyme and the Product (P).

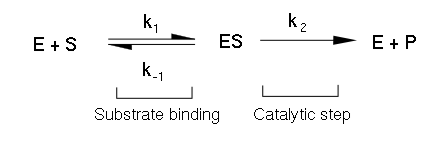
  The above reactions are assumed to be reversible. Here k1, k2, k3, k4 are specific rate constants. Michelis-Menton equation is the rate equation for the reaction catalyzed by an enzyme having a single substrate. In this derivation that the Brigg’s and Halden.

• Molar Concentration of [E] =Concentration of free (or) free (or) uncombined enzyme
• [ES]=Concentration of  Enzyme-Substrate complex
• [Et]=Total enzyme concentration (the sum of the free and combined forms)
• [S]=Concentration of Substrate
• [P]=Concentration of Product

The substrate concentration is assumed to be far greater than the concentration of Enzyme [E]. So that the amount of substrate-bound by the enzyme at any given time is negligible. Compared with the total concentration of [S].

Systematic studies of the effect of substrate concentration on ionic enzyme activity began performing in the late nineteenth century.

Already in 1882, the concept of an enzyme-substrate complex as an intermediary in the process of enzymatic catalysis was introduced. In 1913, Leonor Michaelis (pictured left) and Maud Menten (pictured right) developed this theory and proposed a rate equation that explains the kinetic behavior of the enzyme.

To explain the observed relation between the initial velocity (v₀) and the initial substrate concentration ([S]₀) Michaelis and Menten proposed that the enzymatically catalyzed reactions occur in two phases :

• The first phase: In the first step, the enzyme-substrate complex is formed.
• Second Phase: The enzyme-substrate complex results in the formation of the product, releasing the free enzyme.

In this scheme, k 1 , k 2 and k 3 are constants each individual kinetics of the process and also are called microscopic rate constants . Accordingly, we can say that:

• v ₁ = k ₁ [E] [S]
• v ₂ = k ₂ [ES]
• v ₃ = k ₃ [ES]

One can distinguish between free enzyme (E) and attached to the enzyme substrate (S), so that the total concentration of enzyme , [E _T ], (which is constant throughout the reaction) is:

[E _T ] = [E] + [ES]

As [E] = [ET] – [ES], it follows that:

v ₁ = k ₁ [S] [E _T ] – k ₁ [S] [ES]

This kinetic model adopts the steady-state hypothesis , according to which the concentration of the enzyme-substrate complex is small and constant throughout the reaction (Figure, right).

Therefore, the rate of formation of the enzyme-substrate complex (v 1 ) is equal to that of its dissociation (v 2 + v 3 ):

v ₁ = v ₂ + v ₃

Further, as [ES] is constant, the rate of formation of the products is constant:

v = v ₃ = k ₃ [ES] = constant .

As v 1 = v 2 + v 3 , we can say that:

k 1 [S] [E T ] – k 1 [S] [ES] = k 2 [ES] + k 3 [ES]

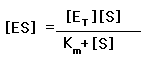
Solving for [ES], is that: being km=(k2+k3) / k1, where the expression (k 2 + k 3 ) / k 1 has been replaced by K M , or Michaelis-Menten constant .

This link gives us an explanation of the reasons that make the K M an important kinetic parameter .

Thus, at steady state, the rate of formation of the product is:

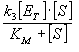
v = v 3 = k 3 [ES]

For any enzyme, [E reaction T], k 3 and KM are constants. Let us consider two extreme cases:

• A small substrate concentrations ([S] << KM ) = v (k3[ET] /KM) [S]. As the terms in parentheses are constant, they can be included in a new constant, kobs, so that the expression is reduced to v = k obs [S], so that the reaction is a first-order kinetic process.
• A high substrate concentrations ([S] >> KM), v = k 3 [E T ] . The reaction rate is independent of the concentration of the substrate, and therefore, the reaction is a zero-order kinetic process. In addition, both k 3 and [E T ] are constant and allows us to define a new parameter, the maximum reaction rate (V max ): V max = k 3 [E T ], which is the rate that would be achieved when all available enzyme bound to the substrate is at.

The Michaelis-Menten equation is the cornerstone of enzyme kinetics, describing the relationship between the reaction rate and substrate concentration.

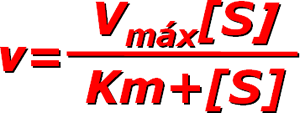
Where:

• V0​ = initial reaction rate
• V_max​ = maximum reaction rate
• [S] = substrate concentration
• K_M = Michaelis constant

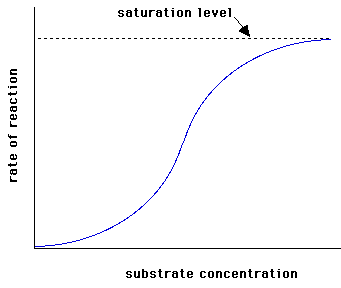
There are enzymes that do not obey the Michaelis-Menten equation. It says it’s not Michaelian kinetics. This happens with Allosteric enzymes, whose graph v vs. [S] is not hyperbole, but a sigmoid (figure right). The Sigmoidal kinetics, small variations in [S] in a critical area (near KM ) results in large variations in the reaction rate.

2. Lineweaver-Burk Plot

The Lineweaver-Burk plot is a double reciprocal graph used to linearize the Michaelis-Menten equation, making it easier to determine VmaxVmax​ and KMKM​.

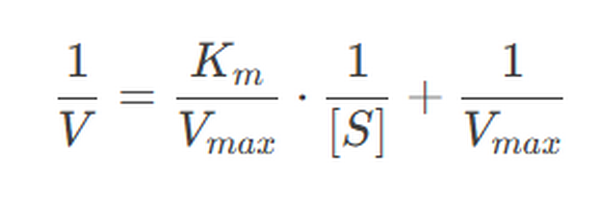
3. Eadie-Hofstee Plot

The Eadie-Hofstee plot is another linearization method, plotting V0V0​ against V0/[S]V0​/[S].

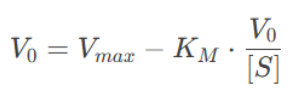
4. Hanes-Woolf Plot

The Hanes-Woolf plot is a third linearization method, plotting [S]/V0[S]/V0​ against [S][S].

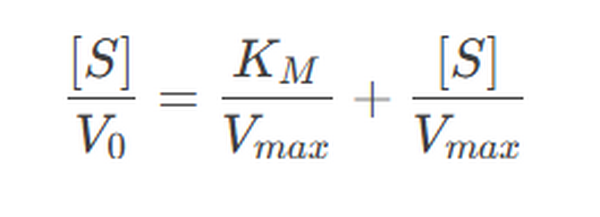
Enzyme Kinetics: Calculation of Km and Vmax

The graphical representation of the Michaelis-Menten equation (v 0 versus [S]0 ) is a hyperbola (figure left). The V max is the maximum value that tends the experimental curve and the KM corresponding to the substrate concentration at which the reaction rate is half of the V max.  To graphically determine the values of Km and Vmax is easier to use the dual representation reciprocal (1/V0 versus 1/[S]0) since it is a straight line. This reciprocal dual representation is called Lineweaver-Burk. It is a line in which:

• The slope is Km/Vmax
• The abscissa at the origin (1/V0 = 0) is -1 /Km
• The intercept (1/[S] 0 = 0) is 1/Vmax

Thus, the experimental data can be calculated graphically, the values of KM and V max of an enzyme for different substrates.

Enzyme Activity

Defines the enzyme unit (U) as the quantity of enzyme that catalyzes the conversion of 1 mol of the substrate in one minute. The specific activity is the number of units of enzyme per milligram of protein (U / mg port) or per milliliter of solution (U / ml).

Recently, the International System of Units (SI) has defined the unit of enzyme activity as the amount of enzyme that converts 1 mol of substrate per second.

This unit is called katal (kat). As 1 mole is 10⁶ pmol and 1 minute is 60 seconds then 1 katal is equivalent to 60 x 10 ⁶ U. 

This unit is very large, so that as the micro-katal sub-multiples (ĩkat, 10 are commonly used ^-6 kat) or nano-katal (nkat 10 ^-9 kat).

When the molecular weight of pure enzyme and the number of active sites per enzyme molecule is known, measurements of enzyme activity to calculate the turnover number of the enzyme, that is, the number of elementary reactions that makes the enzyme active site per and per unit time.

Statement-making of Km an Important Kinetic Parameter

The Michaelis-Menten constant (Km) is an important kinetic parameter for multiple reasons:

• KM is the concentration of the substrate to which the reaction rate is half of the maximum speed. Indeed, if KM = [S], the Michaelis-Menten equation reduces to: v = V max / 2.
• The value of KM suggests the affinity of the enzyme for the substrate: A lower KM , the higher affinity of the enzyme for the substrate, and the higher KM , lower affinity. This fact is easily explained if we consider that KM is defined as (k2+ k3 / k1), where the reactions 2 and 3 destroy the ES complex, while reaction 1 is formed. Thus, if KM is large, the ES complex is unstable because of the prevailing tendency to destroy (low affinity toward the substrate), and if KM is small, the ES complex is stable as a predominant tendency to form it (high affinity toward the substrate).
• The K_M of the natural substrate is less than that of analogous substrates. If two same enzyme substrates have different K_M , which present higher K_M has a lower affinity for the enzyme, and the reaction always takes place more slowly than with the substrate lower K_M , except at saturating substrate concentrations, where v = V_max .
• The values of K_M of many enzymes are close to the physiological concentration of the substrates, so that small variations in the [S] may represent large changes in the speed of the whole metabolic pathway.

Factors Affecting Enzyme Kinetics

1. Substrate Concentration: The rate of an enzymatic reaction increases with substrate concentration until it reaches Vmax​, at which point the enzyme is saturated.
2. Enzyme Concentration: At a constant substrate concentration, the reaction rate is directly proportional to the enzyme concentration.
3. Temperature: Enzyme activity increases with temperature up to an optimal point, beyond which the enzyme denatures, leading to a rapid decline in activity.
4. pH: Each enzyme has an optimal pH at which it functions most efficiently. Deviations from this pH can lead to decreased activity due to changes in the enzyme’s structure.
5. Inhibitors: Inhibitors are molecules that decrease enzyme activity. They can be competitive, non-competitive, or uncompetitive, each affecting the enzyme kinetics differently.
6. Competitive Inhibition: Competitive inhibitors compete with the substrate for the active site, increasing the apparent KM​ without affecting Vmax.
7. Non-Competitive Inhibition: Non-competitive inhibitors bind to a site other than the active site, reducing Vmax​ without affecting KM​.
8. Uncompetitive Inhibition: Uncompetitive inhibitors bind only to the enzyme-substrate complex, decreasing both Vmax​ and KM.
9. Cofactors and Coenzymes: Many enzymes require non-protein molecules called cofactors or coenzymes to function. These can be metal ions or organic molecules that assist in catalysis.

Practical Applications of Enzyme Kinetics

1. Drug Design and Development: Understanding enzyme kinetics is crucial in drug design, particularly in the development of enzyme inhibitors. For example, HIV protease inhibitors are designed based on the kinetics of the HIV protease enzyme.
2. Industrial Biotechnology: Enzyme kinetics is used to optimize industrial processes, such as the production of biofuels, pharmaceuticals, and food products. By understanding and manipulating enzyme kinetics, biotechnologists can enhance yield and efficiency.
3. Clinical Diagnostics: Enzyme activity assays are widely used in clinical diagnostics to detect diseases. For example, elevated levels of certain enzymes in the blood can indicate tissue damage or disease.
4. Metabolic Engineering: Metabolic engineering involves the modification of metabolic pathways to improve the production of desired compounds. Enzyme kinetics provides the tools to understand and optimize these pathways.
5. Environmental Biotechnology: Enzyme kinetics is applied in environmental biotechnology for the degradation of pollutants. Enzymes that break down toxic substances are studied to enhance their efficiency in bioremediation processes.

Advanced Topics in Enzyme Kinetics

1. Allosteric Regulation: Allosteric enzymes have additional regulatory sites where molecules can bind and modulate enzyme activity. This regulation can be positive (activating) or negative (inhibiting).
2. Cooperativity: Cooperativity occurs in multi-subunit enzymes where the binding of a substrate to one subunit affects the binding affinity of other subunits. This is often described by the Hill equation.
3. Enzyme Cascades: Enzyme cascades involve a series of enzymatic reactions where the product of one reaction serves as the substrate for the next. These cascades are crucial in signal transduction pathways.
4. Enzyme Engineering: Enzyme engineering involves the modification of enzymes to enhance their properties, such as stability, activity, and specificity. This is achieved through techniques like directed evolution and rational design.
5. Single-Molecule Enzyme Kinetics: Single-molecule enzyme kinetics studies the behavior of individual enzyme molecules, providing insights into the heterogeneity and dynamics of enzymatic reactions.

Conclusion

Enzyme kinetics is a cornerstone of biochemistry and molecular biology, offering profound insights into the mechanisms of enzymatic reactions. From the fundamental Michaelis-Menten equation to advanced topics like allosteric regulation and enzyme engineering, the study of enzyme kinetics is both broad and deep. Its applications span drug development, industrial biotechnology, clinical diagnostics, and environmental biotechnology, making it an indispensable tool in the life sciences.

By understanding enzyme kinetics, scientists and researchers can manipulate biochemical pathways, design effective drugs, and develop innovative biotechnological solutions. As research in this field continues to advance, the potential for new discoveries and applications is boundless.

References

1. Berg, J. M., Tymoczko, J. L., & Stryer, L. (2015). Biochemistry (8th ed.). W.H. Freeman and Company.
2. Nelson, D. L., & Cox, M. M. (2017). Lehninger Principles of Biochemistry (7th ed.). W.H. Freeman and Company.
3. Fersht, A. (1999). Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. W.H. Freeman and Company.
4. Cornish-Bowden, A. (2012). Fundamentals of Enzyme Kinetics (4th ed.). Wiley-Blackwell.
5. Copeland, R. A. (2000). Enzymes: A Practical Introduction to Structure, Mechanism, and Data Analysis (2nd ed.). Wiley-VCH.